The thermodynamic cost of erasing quantum information: a brief history of demonology

The laws of thermodynamics were forged in the furnaces of the Industrial Revolution, as engineers and scientists refined their picture of energy, studying heat and its interconversion to mechanical work with a view to powering the mines and factories of a new era of human endeavour. Followed by the development of statistical mechanics at the change of the centuries, and far from its practical inception, thermodynamics is now a theory with a remarkable range of applicability, successfully describing the properties of macroscopic systems ranging from refrigerators to black holes. What is unique about thermodynamics is its universality. It has survived the major revolutions of twentieth-century physics and has been a driving force in at least one of them: quantum mechanics. The role thermodynamics has played in the discovery of quantum mechanics, the most successful theory in physics to date, is perhaps under-appreciated. Thermodynamic reasoning was employed in key problems such as black-body radiation studied by Max Planck, and the photo-electric effect that won Albert Einstein the Nobel Prize. These pioneering discoveries ultimately lead to the fully-fledged development of the quantum framework. This universal applicability of thermodynamics was emphasised by Einstein who said thermodynamics is “the only physical theory of universal content, which I am convinced, that within the framework of applicability of its basic concepts will never be overthrown.”

With both the industrial and electronic revolutions behind us, we are currently pushing technology towards and beyond the microscopic scale, right up to the border of where quantum mechanical effects prevail. We are continually finding new ways of manipulating information. Currently, there is interest across a broad range of disciplines in physics surrounding the thermodynamic description of finite quantum systems from both a fundamental and applicative view point. The thriving field of quantum computation tells us that the computers of the future will exploit quantum mechanics in order to grossly out-perform classical machines. This field is now receiving significant attention from some of the largest tech companies in the world as we push towards the age of quantum information. The thermodynamics of these devices will be crucial for long term scalability -  just as heat and dissipation management are key issues for performance on our PCs and laptops that process information. The good news is that although these problems are pragmatic, fascinating fundamental questions arise in theoretical physics while addressing pragmatic problems. My group here at the School of Physics at Trinity, QuSys, focuses on some of these. We work on a range of different topics in quantum physics such as measuring temperature in quantum systems, single atom heat engines, and the origin of thermal behaviour from quantum complexity. However, we have a particular interest in the thermodynamics of quantum systems.

In science it is worth tracking backwards, not only to see where we have come from but also to be humbled by the vastness of what is still unknown. Questions which were posed in the early days of thermodynamics are still inspiring scientists today. The story of thermodynamics begins with the frustration of a Frenchman. Sadi Carnot (pictured right), an aristocratic French military engineer, was convinced that the French defeat in the Napoleonic wars was due to the fact that they had fallen far behind the British from a technological perspective. Steam-engines designed by ingenious engineers were powering a new industrial era in Britain and it particularly irked Carnot that despite the ingenuity of the designs, the engineers did not seem to understand the fundamental physics behind the efficiency of their machines. So he set off on his quest to understand why. In his paper “Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance” (1824), Carnot tackled the essence of the engine’s inner workings and the Carnot Cycle - the prescription for building the most efficient engine – was born. One of the remarkable features of Carnot’s work is that the efficiency of an ideal engine is independent of the material it is made from, depending only on the temperature difference between hot and cold baths. In this result we already see a glimmer of the astounding universal nature of thermodynamics in the independence of the details of the working medium. Carnot’s cycle is by now textbook high school science. Little did he know at the time that the reason for this maximum efficiency was deeply rooted in one of the most famous laws of physics: the second law of thermodynamics.

Despite the brilliance of the work, Carnot’s revelations went largely unnoticed. Carnot died in the cholera epidemic of 1832 in Paris and in 1834 his work was rediscovered by the railroad engineer Emile Clapeyron who used and extended some of Carnot’s ideas. His work was gradually incorporated into the phenomenological theory of thermodynamics which was then taking shape, due largely to the work of Clausius and Belfast-born William Thompson (known as Lord Kelvin). Thermodynamics is basically a set of phenomenological but self-contained laws originally derived empirically from experience. Briefly, the first law of thermodynamics is very simple to understand, and is basically a statement on the conservation of energy that people learn in Junior Cert science. It says that in any process the internal energy change can be divided into the work performed on the system and heat exchanged with the bath. The second law is another story and is far from simple due to the appearance of a dimensionless and often misunderstood quantity known as entropy. In a nutshell, entropy is the physicist’s way of quantifying disorder. The second law tells us that the entropy of every process in the universe, in the absence of external intervention, tends on average to increase and reach a maximum entropy state known as equilibrium. It tells us that when mixed two gases at different temperatures will reach a new state of equilibrium at the average temperature of the two. It is the ultimate law in the sense that every dynamical system is subject to it. There is no escape: all things will reach equilibrium, even you!

These laws were formulated in an empirical way based on experience. This changed due to the paradigm of the atom in science and the beginning of the molecular theory of gases. Around this time people like the Viennese scientist Ludwig Boltzmann and the great Scottish physicist James Clerk Maxwell were formulating the kinetic theory of gases, reviving an old idea of the ancient Greeks by thinking about matter being made of atoms. Although we take it for granted now, at the time it was revolutionary to think about macroscopic observables such as that the pressure of a gas can be understood from the statistical properties of the microscopic constituents - the atoms and molecules comprising it. This is the essential idea of statistical mechanics: macroscopic observables such as the pressure of a gas can be understood as emerging from the microscopic behaviour of a gas.

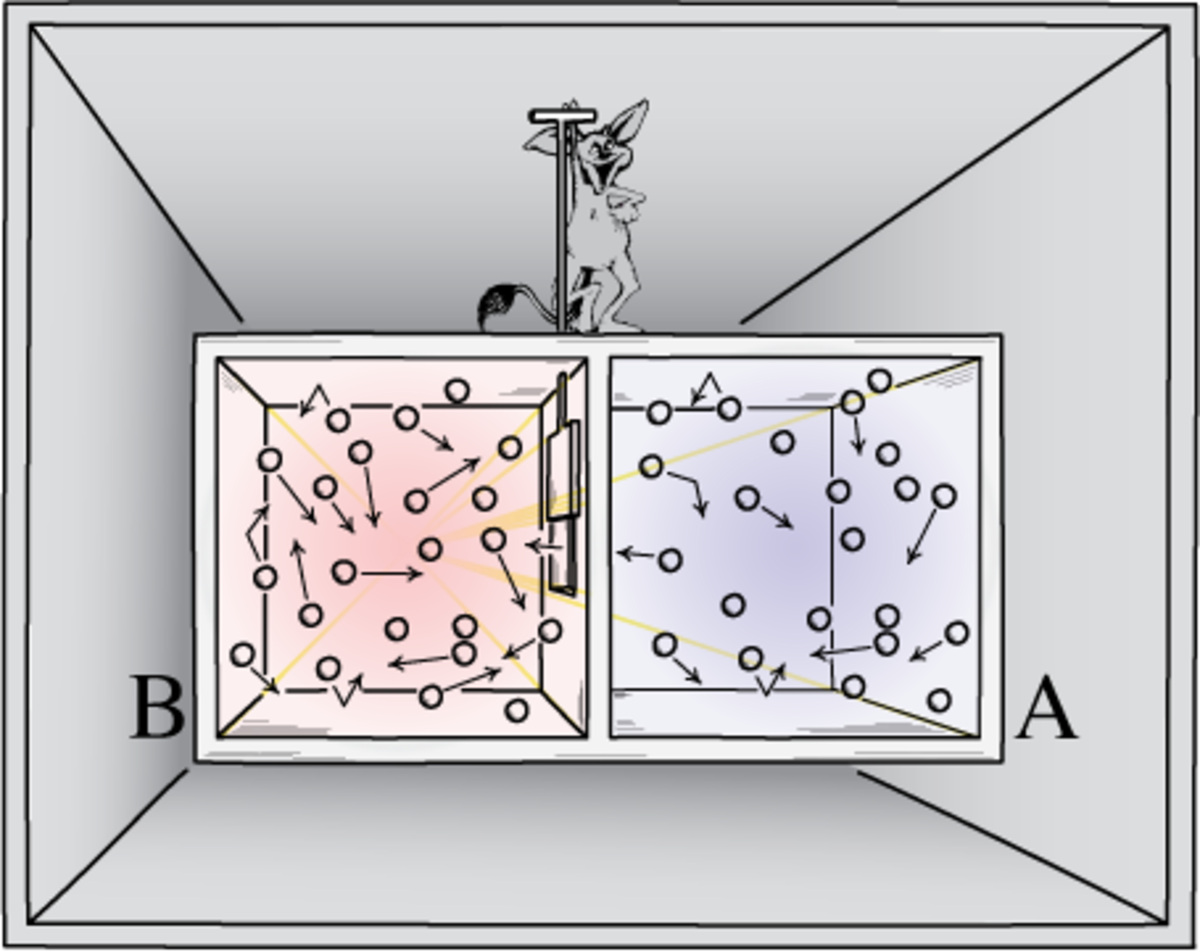Consider the example of two gases at different temperatures brought together. They reach a new, higher entropy state, as prescribed by the second law, at the average temperature. In 1867, James Clerk Maxwell imagined a hypothetical “neat-fingered” being with the ability to track and sort particles in a gas based on their speed. Maxwell’s demon, as the being became known, could quickly open and shut a trap door in a box containing a gas, and let hot particles through to one side of the box but restrict cold ones to the other. At first glance, this scenario seems to contradict the second law of thermodynamics as the overall entropy appears to decrease.  Maxwell’s paradox, which was only properly understood a century after its original inception, continues to inspire physicists. Maxwell’s demon actually got is name from William Thompson in a hugely influential paper published in Nature on the dissipation of energy. With the original Greek meaning of the word in mind, Thompson chose the name not to imply any foul play but rather to emphasise the role of the being’s intelligence, and so perhaps one of the most famous paradoxes in physics was born.

It was 1929 before the next major development in this long story. Stimulated by this abstract notion of intelligence hinted at in Thompson’s essay, the great Hungarian Leo Szilard wrote a paper on the decrease of entropy by intelligent beings (“Uber die Entropiever- minderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen”). In this classic work, Szilard considered a Maxwell’s demon that controlled the thermodynamic cycle of a one-particle heat engine. By making measurements on the system and using the acquired information, the demon could extract work from the closed cycle—once again in apparent contradiction with the second law of thermodynamics. In fact, considering this simple cycle, Szilard was achingly close to resolving the paradox. In short, he believed that there was an entropic penalty caused by the measurements that balanced the work extracted by the demon. Szilard’s work is truly remarkable as it not only marked the beginning of the formal study of the energetics of information processing but also because by reducing Maxwell’s demon to a binary decision problem he predicted the idea of a “bit” - the currency of information. This was decades before information theory was formalised as subject by the engineer Claude Shannon. This incredible foresight was not unusual for Leo Szilard. It is not often appreciated how his genius affected the 20th century. Szilard was the first person to realise the possibility of an atomic bomb, and it was he who convinced Einstein to write together to Roosevelt warning him of the potential danger if this knowledge fell into Nazi hands (the Einstein-Szilard letter ).

Szilard’s work on the role of intelligence in physics continued to inspire physicists through the 20th century, most notably Leon Brillouin who is best known for his work in solid state physics. Brillouin was inspired by Szilard’s idea that a demon was acquiring information and this gave him a lifelong interest in the field of cybernetics. The acquisition of information was also studied by Denis Gabor (sole recipient of Nobel Prize in 1971 for Holography) who again provided evidence that the apparent violation of the second law could be attributed to the energetic cost of the measurement.

In 1961, while working at IBM, Rolf Landauer highlighted the role of logically irreversible operations. As technology for computers was rapidly developing, scientists and engineers began to think deeply about the physics of information processing. Perhaps the most powerful thing about information theory is that it can be formulated independently of any encoding. The reality, however, is summarised best in a mantra which is now irreversibly attached to Landauer: “Information is Physical ”.  In short, information has to be encoded in the physical objects - whether that is lines on a rock, words on a page, or electrons in a transistor. Fundamentally, information is encoded and processed on physical hardware. Information processing can then be broken down to sequences of fundamental operations or logic gates on bits. Landauer’s work split the idea of a computer in to the information bearing degree of freedom - the part of the machine where the information is processed - and the non-information degree of freedom, which is everything else. Fundamental logic operations can be divided into two classes: ones which are logically reversible, and ones which are not. Reversibility means exactly what it says on the tin. If you apply the operation in reverse you go back to the start. For example, think about a logic gate that performs a swap on two bits. You can always swap back.  A logically irreversible operation is something where you cannot know the input from looking at an output. The clear gate, used to erase a bit of information, is an example of this. In a clear gate, all inputs are set to zero (0->0, 1->0). Landauer discovered that when irreversible gate operations are applied then heat is dissipated to the non-information bearing degree of freedom. Where erasure of a single bit of information is concerned he computed the minimal amount of heat dissipated (exactly kTlog2 where k is a constant called Boltzmann’s constant and T is the temperature of the non-information bearing degree of freedom). This is known as the Landauer bound.

 Landauer’s work inspired Charlie Bennett - also of IBM - to investigate the idea of reversible computing and, in so doing, he saw the route to exorcism of Maxwell’s demon. In 1982 Bennett argued that the demon must have a memory, and that it is not the measurement but the erasure of the information of the demon’s memory which is precisely the act which restores the second law in the paradox! This association with the theory of computation was the beginning of a huge amount of work on information thermodynamics. The notion that there is a fundamental lower limit to the heat exchanged in the erasure of information (Landauer’s limit) is firmly entrenched in physics lore. More generally, the association of heat exchange to logical irreversibility is known as Landauer’s principle. But is Landauer’s limit actually relevant for real computers? The answer is, at the moment, not really. The lower bound for heat exchange is a really small quantity of energy, and actual computers dissipate far more than this when erasing their registers. However, it is still important to think about the bound as the miniaturisation of computing components continues; the bound becomes closer and it may well become even more relevant for quantum computing machines.

Exciting recent developments have seen fundamental experiments devised which are now able to study single bit erasure close to Landauer’s limit. Only recently the first experiment measuring heat exchange at this limit was performed. In this experiment, performed in 2012, a bit of information was encoded in the position on either side of the barrier of an optically trapped microscopic particle. As noted earlier, a bit (0 or 1) can be encoded in many different ways and here it is encoded on the left or right of the barrier. The challenge here is that at this microscopic level, the particle is very prone to what we call thermal fluctuations. Thermal fluctuations are noise from the environment which give the particle some random chance to get energy from the background and jump over the barrier. In physics we say that the system is stochastic. In such a setting one has to be careful about the way thermodynamics is formulated and this is a topic that is of great interest to my own work. What stochastic thermodynamics tells us is that the usual thermodynamic quantities are described by probability distributions, whose mean values correspond to the quantities studied in thermodynamics such as entropy and heat. The wonderful thing about this experiment is that by manipulating the container that the microscopic particle is contained in (with light fields), a single bit erasure could be performed and the full distribution of heat values could be observed. The experiment demonstrated that if the erasure process was carried out slowly enough then, on average, you found that Landauer’s prediction for the heat exchanged was precisely met. What was also observed is that, due to the probabilistic nature of heat exchange at this level, there were some instances where Landauer’s bound was seemingly violated. However, if the experiment is repeated and an average is taken, it is restored. These transient events are rare and become even rarer as temperature is increased.

My group recently became very interested in what happens if precisely the same experiment is performed but now the particle obeys the laws of quantum mechanics. This paper has recently been accepted for publication in Physical Review Letters. We are currently in a period where technology is being developed which is based on the laws of quantum mechanics. While the fundamental unit for information is the bit, quantum mechanics has the qubit and the weird thing about quantum mechanics is that it allows for something called superposition which allows the qubit to be in both states 0 and 1 at the same time. In this work, along with collaborator Harry Miller at the University of Manchester and two postdoctoral researchers in my own group at Trinity, Mark Mitchison and Giacomo Guarnieri, we consider the experiment above on erasing a bit of information, only this time we allow for quantum superposition. This means that our particle can be both left and right of the barrier at the same time. Pretty weird but this is quantum mechanics after all! The question we asked is what difference does this distinctly quantum feature make for the erasure protocol? We got something we did not expect! We found that due to superposition you get very rare events with heat exchanges far greater than the Landauer limit. In the paper we prove mathematically that these events exist and are a uniquely quantum feature. This is a highly unusual finding and is actually an example of an effect that could be really important for heat management on future quantum chips. However, there is much more work to be done in particular to analyse faster operations and the thermodynamics of other gate implementations. One thing is for certain though: 150 years later, the legacy of Maxwell’s demon is still going strong.